Simple beam - Uniform load partially distributed Calculator

Deflection Yac:

Deflection Ycd:

Deflection Ydb:

Slope θac:

Slope θcd:

Slope θdb:

Moment Mac:

Moment Mcd:

Moment Mdb:

Shear Vac:

Shear Vcd:

Shear Vdb:

Shear Va:

Shear Vb:

Shear Vc:

Shear Vd:

Reactions Ra:

Reactions Rb:

α:

β:

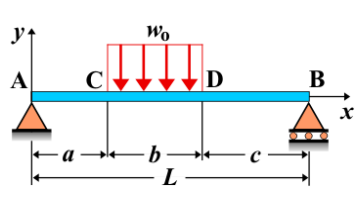
Simple Beam - Uniform Load Partially Distributed

A simple beam is supported at both ends, with a uniform load applied over a specific portion of its length. The load distribution can be anywhere along the beam, affecting the shear force, bending moment, and deflection in a distinct manner compared to a fully distributed load.

Key Concepts

Simple Beam: A beam supported at both ends, allowing rotation but preventing vertical displacement.
Partially Distributed Load: A uniform load covering only a section of the beam, rather than the entire span.
Shear Force: The shear force varies depending on the position and extent of the distributed load. It changes abruptly at the points where the load begins and ends.
Bending Moment: The bending moment is influenced by the length and location of the distributed load, reaching a maximum value somewhere along the beam.
Deflection: The beam's deflection will be most pronounced in the loaded section, with the exact shape depending on the location and magnitude of the load.

Behavior of the Simple Beam

Reaction Forces:
- The total equivalent force of the distributed load is its intensity multiplied by its length.
- The reactions at the supports are calculated based on equilibrium equations, considering the load's position and length.
Shear Force Diagram:
- The shear force varies linearly in the unloaded sections and changes more noticeably within the loaded section.
- There is a discontinuity in the slope of the shear force diagram at the start and end of the distributed load.
Bending Moment Diagram:
- The bending moment increases within the loaded region, reaching a peak depending on the load’s position and length.
- The moment diagram has different slopes before, within, and after the loaded section.
Deflection: The deflection is most pronounced in the region affected by the distributed load. The exact value depends on the beam's material, cross-section, and load parameters.

Applications

Structural Engineering: Used in bridge and floor beam designs where loads are applied over partial spans.
Mechanical Systems: Found in machine components subject to localized loading, such as conveyor systems.
Construction: Relevant for analyzing beams subjected to unevenly distributed loads from walls, roofing, or storage.

Formula

Quantity	Formula
Deflection \(y_{AC}\)	\(\frac{R_{A}x^{3}}{6EI} + \alpha x\)
Deflection \(y_{CD}\)	\(\frac{R_{A}x^{3}}{6EI} - \frac{w_{0}}{24EI}(x-a)^{4} + \alpha x\)
Deflection \(y_{DB}\)	\(\frac{R_{B}(L-x)^{3}}{6EI} + \frac{\beta (L-x)}{L}\)
Slope \(\theta_{AC}\)	\(\frac{R_{A}x^{2}}{2EI} + \alpha\)
Slope \(\theta_{CD}\)	\(\frac{R_{A}x^{2}}{2EI} - \frac{w_{0}}{6EI}(x-a)^{3} + \alpha\)
Slope \(\theta_{DB}\)	\(\frac{-R_{B}(L-x)^{2}}{2EI} - \frac{\beta}{L}\)
Moment \(M_{AC}\)	\(R_{A} x\)
Moment \(M_{CD}\)	\(R_{A} x - \frac{w_{0}}{2}(x-a)^{2}\)
Moment \(M_{DB}\)	\(R_{B}(L-x)\)
Shear \(V_{AC}, V_{A}, V_{C}\)	\(R_{A}\)
Shear \(V_{CD}\)	\(R_{A} - w_{0}(x-a)\)
Shear \(V_{DB}, V_{D}, V_{B}\)	\(-R_{B}\)
Reaction \(R_{A}\)	\(\frac{w_{0}b}{2L}(2c+b)\)
Reaction \(R_{B}\)	\(\frac{w_{0}b}{2L}(2a+b)\)
\(\alpha\)	\(\frac{w_{0}b^{3}L - 6EI\beta - 3R_{B}c^{2}L - 3R_{A}L(a+b)^{2}}{6LEI}\)
\(\beta\)	\(\frac{4w_{0}ab^{3} + 3w_{0}b^{4} - 8R_{A}(a+b)^{3} - 12R_{B}c^{2}L + 8R_{B}c^{3}}{24EI}\)

Definitions

Symbol	Physical quantity	Units
E·I	Flexural rigidity	N·m², Pa·m⁴
y	Deflection or deformation	m
θ	Slope, Angle of rotation	-
x	Distance from support (origin)	m
L	Length of beam (without overhang)	m
M	Moment, Bending moment, Couple moment applied	N·m
P	Concentrated load, Point load, Concentrated force	N
w	Distributed load, Load per unit length	N/m
R	Reaction load, reaction force	N
V	Shear force, shear	N