Simple beam - Uniform load partially distributed at left end (I) Calculator
Simple Beam - Uniform Load Partially Distributed at Left End (I)
A simple beam is supported at both ends, with a uniform load partially distributed at the left end of the beam. The load is applied over a certain length starting from the left support, with the magnitude of the load being constant along the length of the distribution. The distribution of this load affects the shear force, bending moment, and deflection along the beam, particularly closer to the left end.
Key Concepts
- Simple Beam: A beam supported at both ends, with no intermediate supports.
- Uniform Load: A distributed load that is constant along the length it covers. In this case, it is applied at the left end and extends partially along the beam.
- Shear Force: The shear force is greatest near the left support, where the load is applied. As you move away from the left support, the shear force gradually decreases until the end of the load distribution.
- Bending Moment: The bending moment is highest near the left support and decreases along the length of the beam. The bending moment is influenced by the magnitude and length of the uniform load at the left end.
- Deflection: The deflection is greatest near the left end where the load is applied. The beam will bend more near this end, and the deflection will decrease as you move toward the right end.
Behavior of the Simple Beam
- Reaction Forces:
- The total load applied at the left end is the product of the load intensity and the length of the distribution. The reaction forces at both supports are calculated using equilibrium conditions. The reaction at the left support will be larger than the reaction at the right support due to the location of the load.
- Shear Force Diagram:
- The shear force diagram shows a linear decrease from the left support towards the end of the load distribution. The shear force is maximum at the left support and gradually reduces to zero at the point where the load distribution ends.
- Bending Moment Diagram:
- The bending moment is highest at the left support, where the load is applied. The moment decreases along the length of the load distribution, and the moment diagram will have a curve indicating this change.
- Deflection: The deflection is greatest near the left support, where the load is applied. The deflection curve is steeper in this region and gradually flattens as you move further from the left end.
Applications
- Structural Engineering: This type of loading is commonly encountered in beams where the load is applied closer to one support, such as in bridges or floor beams with localized loads.
- Mechanical Systems: Found in mechanical components where forces are applied over a partial length, such as supports for machinery or conveyor systems with varying loads.
- Construction: Relevant in the analysis of beams where the load is concentrated near one end, such as in cantilevered beams or roofs with localized loading at the supports.
Formula
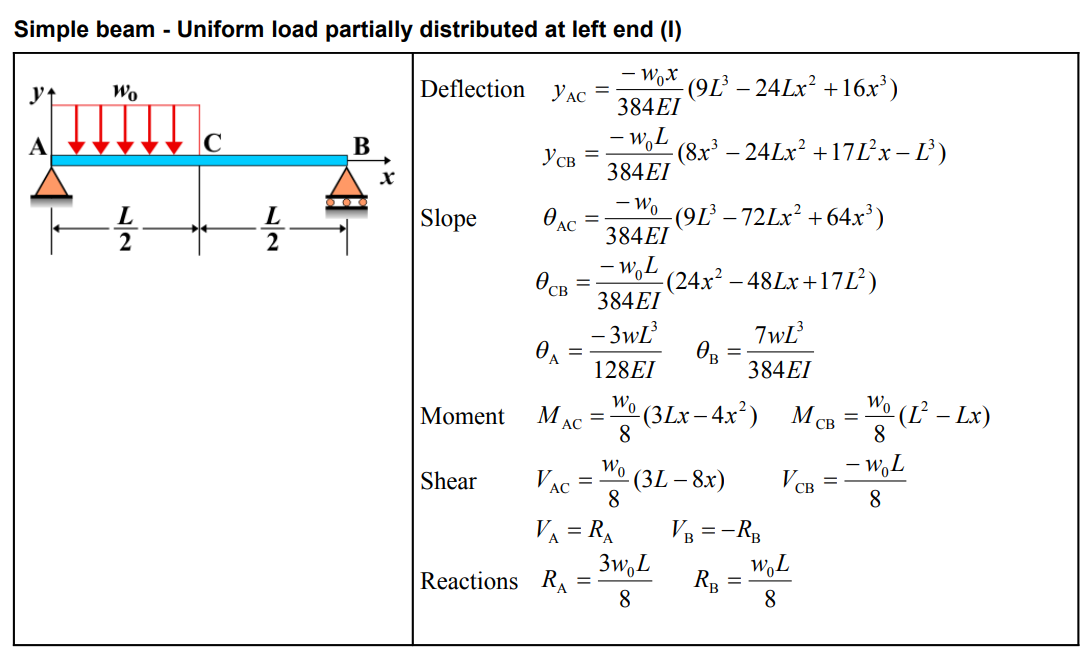
| Quantity | Formula |
|---|---|
| Deflection \(y_{AC}\) | \(-\frac{w_0 x}{384EI} \left(9L^3 - 24Lx^2 + 16x^3 \right)\) |
| Deflection \(y_{CB}\) | \(-\frac{w_0 L}{384EI} \left(8x^3 - 24Lx^2 + 17L^2x - L^3 \right)\) |
| Slope \(\theta_{AC}\) | \(-\frac{w_0}{384EI} \left(9L^3 - 72Lx^2 + 64x^3 \right)\) |
| Slope \(\theta_{CB}\) | \(-\frac{w_0 L}{384EI} \left(24x^2 - 48Lx + 17L^2 \right)\) |
| \(\theta_A\) | \(-\frac{3w_0 L^3}{128EI}\) |
| \(\theta_B\) | \(\frac{7w_0 L^3}{384EI}\) |
| Moment \(M_{AC}\) | \(\frac{w_0}{8} \left(3Lx - 4x^2 \right)\) |
| Moment \(M_{CB}\) | \(\frac{w_0}{8} \left(L^2 - Lx \right)\) |
| Shear \(V_{AC}\) | \(\frac{w_0}{8} \left(3L - 8x \right)\) |
| Shear \(V_{CB}\) | \(-\frac{w_0 L}{8}\) |
| \(V_A = R_A\) | \(\frac{3w_0 L}{8}\) |
| \(V_B = -R_B\) | \(-\frac{w_0 L}{8}\) |
| Reactions \(R_A\) | \(\frac{3w_0 L}{8}\) |
| Reactions \(R_B\) | \(\frac{w_0 L}{8}\) |
Definitions
| Symbol | Physical quantity | Units |
|---|---|---|
| E·I | Flexural rigidity | N·m², Pa·m⁴ |
| y | Deflection or deformation | m |
| θ | Slope, Angle of rotation | - |
| x | Distance from support (origin) | m |
| L | Length of beam (without overhang) | m |
| M | Moment, Bending moment, Couple moment applied | N·m |
| P | Concentrated load, Point load, Concentrated force | N |
| w | Distributed load, Load per unit length | N/m |
| R | Reaction load, reaction force | N |
| V | Shear force, shear | N |
 Home
Home Back
Back