Simple beam - Load increasing uniformly to center Calculator
Simple Beam - Load Increasing Uniformly to Center
A simple beam is supported at both ends, with a distributed load that increases uniformly from one end to the center of the beam. This type of load distribution creates varying shear force and bending moment along the beam's length. The load intensity is zero at the left end and increases linearly to a maximum value at the center of the beam, and then decreases symmetrically towards the right support.
Key Concepts
- Simple Beam: A beam supported at both ends, with no intermediate supports.
- Linearly Increasing Load: The load intensity starts from zero at one end and increases linearly to a maximum value at the center, after which it decreases symmetrically to zero at the other end.
- Shear Force: The shear force varies nonlinearly along the length of the beam, increasing from zero at the left support to a maximum at the center, and then decreasing back to zero at the right support.
- Bending Moment: The bending moment is maximum at the center of the beam, where the load intensity is highest. The moment increases as the load increases and decreases as the load diminishes towards the right support.
- Deflection: The maximum deflection occurs at the center of the beam, where the bending moment is largest. The deflection shape follows the curve of the load distribution.
Behavior of the Simple Beam
- Reaction Forces:
- The total load on the beam can be calculated by finding the area under the load distribution. The reactions at the supports are determined by summing the vertical forces and considering the equilibrium of moments.
- Shear Force Diagram:
- The shear force increases from zero at the left support, reaches a maximum value at the center of the beam, and then decreases back to zero at the right support.
- Bending Moment Diagram:
- The bending moment increases quadratically along the length of the beam, reaching its maximum value at the center, where the load intensity is greatest.
- Deflection: The deflection is maximum at the center of the beam, where the bending moment is greatest. The deflection can be calculated using beam deflection formulas that depend on the beam’s length, the load distribution, and material properties.
Applications
- Structural Engineering: This type of loading is common in structures subjected to wind pressure, soil pressure, or other environmental forces that vary in intensity over the length of the beam.
- Mechanical Systems: Found in components experiencing varying loads, such as mechanical parts that are subjected to forces that increase towards the center.
- Construction: Used in the analysis of beams in buildings and other structures that experience distributed loads which increase towards the center, such as beams in bridges or floors.
Formula
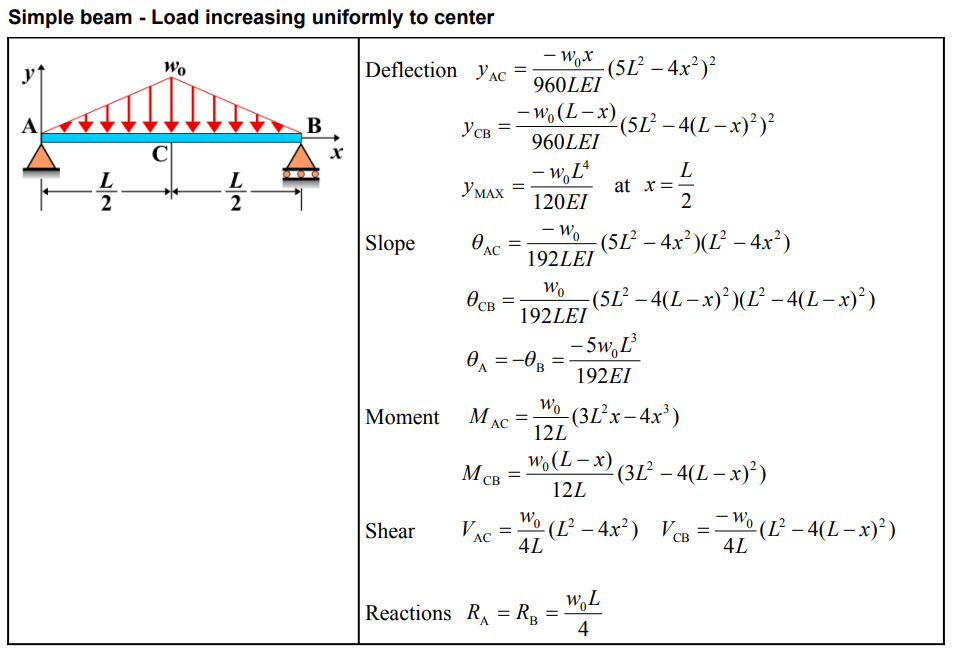
| Deflection (AC) | \[ y_{\mathrm{AC}} = \frac{-w_0 x}{960 L E I}\left(5 L^2 - 4 x^2\right)^2 \] |
| Deflection (CB) | \[ y_{\mathrm{CB}} = \frac{-w_0(L-x)}{960 L E I}\left(5 L^2 - 4 (L-x)^2\right)^2 \] |
| Maximum Deflection | \[ y_{\mathrm{MAX}} = \frac{-w_0 L^4}{120 E I} \quad \text{at} \quad x = \frac{L}{2} \] |
| Slope | No slope formula provided in the text |
| Moment (AC) | \[ M_{\mathrm{AC}} = \frac{w_0}{12 L}\left(3 L^2 x - 4 x^3\right) \] |
| Moment (CB) | \[ M_{\mathrm{CB}} = \frac{w_0(L-x)}{12 L}\left(3 L^2 - 4 (L-x)^2\right) \] |
| Shear (AC) | \[ V_{\mathrm{AC}} = \frac{w_0}{4 L}\left(L^2 - 4 x^2\right) \] |
| Shear (CB) | \[ V_{\mathrm{CB}} = \frac{-w_0}{4 L}\left(L^2 - 4 (L-x)^2\right) \] |
| Reactions | \( R_{\mathrm{A}} = R_{\mathrm{B}} = \frac{w_0 L}{4} \) |
Definitions
| Symbol | Physical quantity | Units |
|---|---|---|
| E·I | Flexural rigidity | N·m², Pa·m⁴ |
| y | Deflection or deformation | m |
| θ | Slope, Angle of rotation | - |
| x | Distance from support (origin) | m |
| L | Length of beam (without overhang) | m |
| M | Moment, Bending moment, Couple moment applied | N·m |
| P | Concentrated load, Point load, Concentrated force | N |
| w | Distributed load, Load per unit length | N/m |
| R | Reaction load, reaction force | N |
| V | Shear force, shear | N |
 Home
Home Back
Back