Simple beam - Concentrated load at any point Calculator

Deflection Yac:

Deflection Ycb:

Slope θac:

Slope θcb:

Slope θa:

Slope θb:

Moment Mac:

Moment Mcb:

Shear Vac:

Shear Vcb:

Shear Va:

Shear Vb:

Reactions Ra:

Reactions Rb:

Simple Beam - Concentrated Load at Any Point

A simple beam is a beam that is supported at both ends, typically with one or both ends free to rotate and translate. When a concentrated load is applied at any point along the length of the beam, it creates internal forces and deformations. The load produces shear forces and bending moments that vary along the beam, with specific reactions at the supports and a bending moment that reaches a maximum at the point of application of the load.

Key Concepts

Simple Beam: A beam supported at both ends, with no intermediate supports.
Concentrated Load: A load applied at a specific point on the beam, which generates localized forces and moments.
Shear Force: The shear force is greatest at the supports and changes at the location where the load is applied. The shear force at the point of application of the concentrated load will have a discontinuity, shifting from one value to another.
Bending Moment: The bending moment diagram will show a linear variation from the left support to the point of application of the load, where it reaches a maximum, and then a linear decrease toward the right support.
Deflection: The deflection occurs along the length of the beam, with the maximum deflection occurring at the point where the load is applied. The magnitude of deflection is influenced by the load magnitude, beam length, and material properties.

Behavior of the Simple Beam

Reaction Forces:
- The reactions at the supports are calculated using equilibrium equations. These reactions depend on the magnitude and location of the concentrated load.
Shear Force Diagram:
- The shear force diagram shows a jump at the location where the concentrated load is applied. The shear force will be constant on either side of the load and will change suddenly at the point where the load acts.
Bending Moment Diagram:
- The bending moment diagram is linear between the supports, increasing from the left support to the point of application of the load, where it reaches its maximum value. After the load point, the moment decreases linearly toward the right support.
Deflection: The maximum deflection occurs at the point of application of the concentrated load and can be calculated using beam deflection formulas. The deflection depends on the magnitude of the load, the distance from the supports, the modulus of elasticity, and the moment of inertia of the beam.

Applications

Structural Engineering: Simple beams with concentrated loads are used in a wide range of applications, including bridges, floors, and frames where point loads act on the beam.
Construction: Used in building construction where loads are applied at specific points along the beam length, such as heavy machinery or concentrated loads from columns or walls.
Mechanical Systems: Found in mechanical systems where concentrated loads are applied to beams or supports, such as in frames or load-bearing structures.

Formula

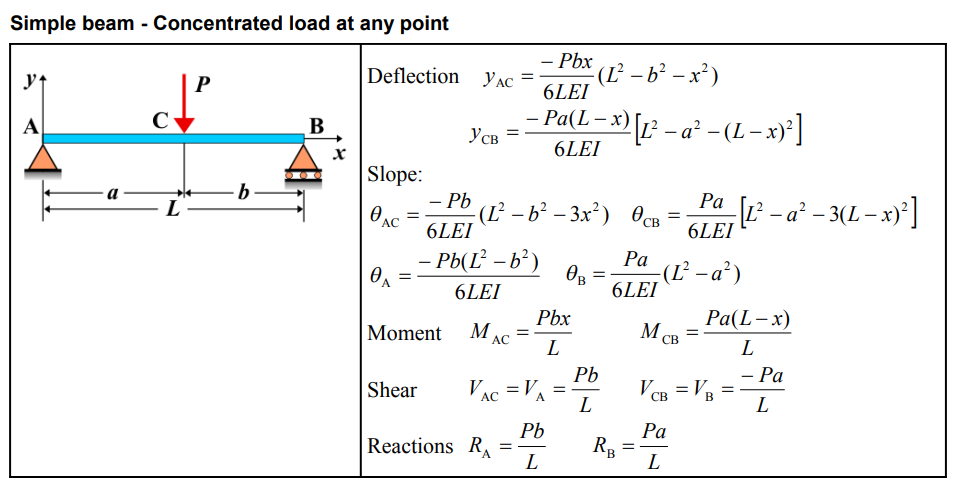
Deflection (AC)	\( y_{\mathrm{AC}} = \frac{-Pbx}{6LEI}(L^{2}-b^{2}-x^{2}) \)
Deflection (CB)	\( y_{\mathrm{CB}} = \frac{-Pa(L-x)}{6LEI}\left[L^{2}-a^{2}-(L-x)^{2}\right] \)
Slope (AC)	\( \theta_{\mathrm{AC}} = \frac{-Pb}{6LEI}(L^{2}-b^{2}-3x^{2}) \)
Slope (CB)	\( \theta_{\mathrm{CB}} = \frac{Pa}{6LEI}\left[L^{2}-a^{2}-3(L-x)^{2}\right] \)
Slope at A	\( \theta_{\mathrm{A}} = \frac{-Pb(L^{2}-b^{2})}{6LEI} \)
Slope at B	\( \theta_{\mathrm{B}} = \frac{Pa}{6LEI}(L^{2}-a^{2}) \)
Moment (AC)	\( M_{\mathrm{AC}} = \frac{Pbx}{L} \)
Moment (CB)	\( M_{\mathrm{CB}} = \frac{Pa(L-x)}{L} \)
Shear (AC)	\( V_{\mathrm{AC}} = V_{\mathrm{A}} = \frac{Pb}{L} \)
Shear (CB)	\( V_{\mathrm{CB}} = V_{\mathrm{B}} = \frac{-Pa}{L} \)
Reactions (A)	\( R_{_A} = \frac{Pb}{L} \)
Reactions (B)	\( R_{_B} = \frac{Pa}{L} \)