Fixed-fixed beam - Two equal concentrated loads symmetrically placed Calculator
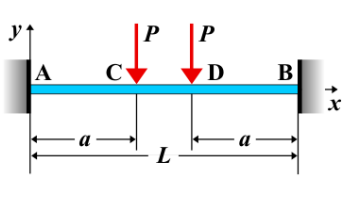
Fixed-Fixed Beam - Two Equal Concentrated Loads Symmetrically Placed
A fixed-fixed beam is a beam that is rigidly supported at both ends. When **two equal concentrated loads** are applied symmetrically along the beam, the loads create a bending moment and shear force distribution that is symmetric about the center of the beam. The concentrated loads induce reactions at the supports, and the beam bends under the action of these loads.
Key Concepts
- Equal Concentrated Loads: Two loads of equal magnitude, \( P \), applied at equal distances from the center of the beam, creating a symmetric loading condition.
- Symmetric Loading: The loads are placed symmetrically with respect to the center of the beam, resulting in a symmetric distribution of bending moments and shear forces.
- Fixed-Fixed Beam: A beam that is rigidly fixed at both ends, preventing both translational and rotational displacements at the supports.
- Shear Force: The shear force distribution is symmetric and linear along the beam, with maximum shear force at the supports.
- Bending Moment: The bending moment increases from the supports towards the center of the beam and reaches a maximum at the center of the beam.
- Deflection: The deflection of the beam is influenced by the applied loads and the beam's stiffness, and it is symmetric about the center of the beam.
Behavior of the Fixed-Fixed Beam
- Reaction Forces:
- The total applied load \( 2P \) is distributed equally between the two supports. Each support reaction is equal to \( R = P \), due to the symmetry of the load distribution.
- The reactions at the supports are vertical forces, and there are no moments at the supports since the beam is fixed at both ends.
- Shear Force Diagram:
- The shear force distribution is linear and symmetric, with maximum shear force occurring at the supports.
- At the center of the beam, the shear force is zero because the two loads cancel each other out.
- Bending Moment Diagram:
- The bending moment distribution is parabolic, increasing from zero at the supports to a maximum at the center of the beam.
- The maximum bending moment at the center of the beam is given by: \[ M_{\text{max}} = \frac{P L}{4} \] where \( P \) is the applied concentrated load, and \( L \) is the length of the beam.
- The bending moment is symmetric about the center and zero at the supports.
- Deflection: The deflection is maximum at the center of the beam and is given by: \[ \delta_{\text{max}} = \frac{P L^3}{48 E I} \] where \( P \) is the concentrated load, \( L \) is the length of the beam, \( E \) is the modulus of elasticity, and \( I \) is the moment of inertia of the beam's cross-section.
Applications
- Structural Engineering: Common in beams supporting symmetric loads, such as bridges, platforms, and floors under uniform loading conditions.
- Construction: Relevant in beams supporting symmetric equipment or structural elements in buildings and other infrastructure.
- Mechanical Systems: Found in systems where symmetric loads are applied, such as components subjected to forces in machines or vehicles.
Formula

| Quantity | Formula |
|---|---|
| Deflection \(y_{AC}\) | \[ y_{AC} = \frac{-Px^2}{6EIL} \left(3aL - 3a^2 - Lx\right) \] |
| Deflection \(y_{CD}\) | \[ y_{CD} = \frac{-Pa^2}{6EIL} \left(3Lx - 3x^2 - aL\right) \] |
| Deflection \(y_{DB}\) | \[ y_{DB} = \frac{-P(L-x)^2}{6EIL} \left(3aL - 3a^2 - L(L-x)\right) \] |
| Slope \(\theta_{AC}\) | \[ \theta_{AC} = \frac{-Px}{2EIL} \left(2aL - 2a^2 - Lx\right) \] |
| Slope \(\theta_{CD}\) | \[ \theta_{CD} = \frac{-Pa^2}{2EIL} \left(L - 2x\right) \] |
| Slope \(\theta_{DB}\) | \[ \theta_{DB} = \frac{P(L-x)}{2EIL} \left[2aL - 2a^2 - L(L-x)\right] \] |
| Moment \(M_{AC}\) | \[ M_{AC} = \frac{P}{L} \left(Lx - aL + a^2\right) \] |
| Moment \(M_{CD}\) | \[ M_{CD} = \frac{Pa^2}{L} \] |
| Moment \(M_{DB}\) | \[ M_{DB} = \frac{P}{L} \left(L^2 - Lx - La + a^2\right) \] |
| Shear \(V_{AC}\) | \[ V_{AC} = P \] |
| Shear \(V_{CD}\) | \[ V_{CD} = 0 \] |
| Shear \(V_{DB}\) | \[ V_{DB} = -P \] |
| Reactions \(R_A = R_B\) | \[ R_A = R_B = P \] |
Definitions
| Symbol | Physical quantity | Units |
|---|---|---|
| E·I | Flexural rigidity | N·m², Pa·m⁴ |
| y | Deflection or deformation | m |
| θ | Slope, Angle of rotation | - |
| x | Distance from support (origin) | m |
| L | Length of beam (without overhang) | m |
| M | Moment, Bending moment, Couple moment applied | N·m |
| P | Concentrated load, Point load, Concentrated force | N |
| w | Distributed load, Load per unit length | N/m |
| R | Reaction load, reaction force | N |
| V | Shear force, shear | N |
 Home
Home Back
Back