Fixed-fixed beam - Concentrated load at center Calculator
Fixed-Fixed Beam - Concentrated Load at Center
A fixed-fixed beam is a beam that is rigidly supported at both ends, preventing rotation and translation. When a concentrated load is applied at the center of the beam, the load acts as a point force, and the beam's behavior, including shear force, bending moment, and deflection, depends on the location and magnitude of this load.
Key Concepts
- Concentrated Load at Center: A load applied exactly at the midpoint of the beam. It causes symmetrical shear force and bending moment distributions on both sides of the beam.
- Fixed-Fixed Beam: A beam supported at both ends with fixed supports, which prevent any displacement or rotation at the supports.
- Shear Force: The shear force is constant to the left and right of the center of the beam, but it changes at the load application point, creating a jump in the shear force diagram.
- Bending Moment: The bending moment is symmetrical and is maximum at the center of the beam, where the load is applied.
- Deflection: The maximum deflection occurs at the center of the beam and is influenced by the magnitude of the concentrated load and the beam's properties.
Behavior of the Fixed-Fixed Beam
- Reaction Forces:
- At each fixed support, a reaction force is developed to balance the applied load. Since the load is applied at the center, the reaction forces at both supports are equal in magnitude, each being half of the total applied load, \( \frac{P}{2} \).
- Shear Force Diagram:
- The shear force remains constant on each side of the load and then changes direction at the point of application.
- The maximum shear force occurs just at the supports and is equal to \( \frac{P}{2} \) at both ends.
- Bending Moment Diagram:
- The bending moment is highest at the center of the beam, where the load is applied, and decreases towards the supports.
- The maximum bending moment at the center of the beam is given by: \[ M_{\text{max}} = \frac{P L}{4} \] where \( P \) is the concentrated load and \( L \) is the length of the beam.
- The bending moment is zero at both supports and increases to its maximum at the center.
- Deflection: The deflection at the center of the beam is given by the standard formula for a beam with a concentrated load at the center: \[ \delta_{\text{max}} = \frac{P L^3}{48 E I} \] where \( P \) is the concentrated load, \( L \) is the length of the beam, \( E \) is the modulus of elasticity, and \( I \) is the moment of inertia of the beam's cross-section.
Applications
- Structural Engineering: Common in beams subjected to central point loads, such as beams in bridges, floors, and frames.
- Mechanical Systems: Used in components where a concentrated load is applied at the center, such as shafts, arms, or supports in machinery.
- Construction: Relevant in the analysis of beams that support central point loads, such as beams carrying walls or equipment in buildings.
Formula
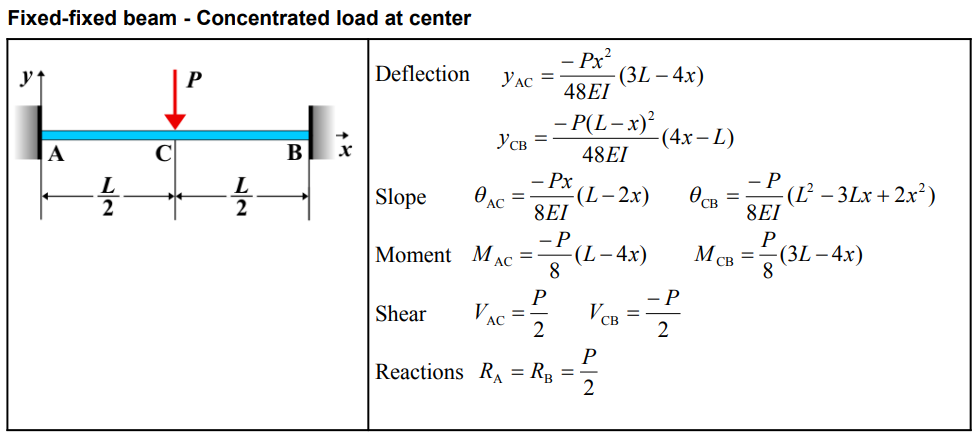
| Parameter | Formula |
|---|---|
| Deflection (AC) | \( y_{AC} = \frac{-P x^2 (3L - 4x)}{48EI} \) |
| Deflection (CB) | \( y_{CB} = \frac{-P (L - x)^2 (4x - L)}{48EI} \) |
| Slope (AC) | \( \theta_{AC} = \frac{-P x (L - 2x)}{8EI} \) |
| Slope (CB) | \( \theta_{CB} = \frac{-P (L^2 - 3Lx + 2x^2)}{8EI} \) |
| Moment (AC) | \( M_{AC} = \frac{-P (L - 4x)}{8} \) |
| Moment (CB) | \( M_{CB} = \frac{P (3L - 4x)}{8} \) |
| Shear (AC) | \( V_{AC} = \frac{P}{2} \) |
| Shear (CB) | \( V_{CB} = \frac{-P}{2} \) |
| Reactions | \( R_A = R_B = \frac{P}{2} \) |
Definitions
| Symbol | Physical quantity | Units |
|---|---|---|
| E·I | Flexural rigidity | N·m², Pa·m⁴ |
| y | Deflection or deformation | m |
| θ | Slope, Angle of rotation | - |
| x | Distance from support (origin) | m |
| L | Length of beam (without overhang) | m |
| M | Moment, Bending moment, Couple moment applied | N·m |
| P | Concentrated load, Point load, Concentrated force | N |
| w | Distributed load, Load per unit length | N/m |
| R | Reaction load, reaction force | N |
| V | Shear force, shear | N |
 Home
Home Back
Back