Cantilever beam - Uniform load partially distributed at free end Calculator
Cantilever Beam - Uniform Load Partially Distributed at Free End
A cantilever beam is a structural element that is fixed at one end and free at the other. When a **uniformly distributed load** is applied to only a portion of the beam, starting from the free end and extending a length \( b \) towards the fixed end, it results in a different distribution of shear force, bending moment, and deflection compared to a uniformly distributed load applied across the entire beam length.
Key Concepts
- Uniform Load: A constant load intensity, \( w \), applied uniformly along a section of the beam, starting from the free end and extending a length \( b \) towards the fixed end.
- Fixed End: The end of the beam that is rigidly attached to a support, preventing both rotation and translation.
- Free End: The unsupported end of the beam, where the load is applied.
- Shear Force: The shear force is influenced by the uniformly distributed load, and it gradually increases as you move towards the fixed end of the beam.
- Bending Moment: The bending moment increases linearly over the length of the distributed load and reaches a maximum at the fixed end of the beam.
- Deflection: The deflection of the beam is most significant near the free end where the load is applied, and the maximum deflection occurs closer to the free end.
Behavior of the Cantilever Beam
- Reaction Forces:
- At the fixed end, the total equivalent load from the uniform load distribution is equal to \( w \cdot b \), where \( w \) is the load intensity and \( b \) is the length of the loaded portion of the beam.
- A reaction moment \( M_A \) is developed to counterbalance the applied load, which is influenced by the location and intensity of the distributed load.
- Shear Force Diagram:
- The shear force increases gradually along the beam, with the rate of increase being proportional to the intensity and length of the distributed load.
- The maximum shear force occurs at the fixed end and is given by \( V_A = w \cdot b \), where \( b \) is the length of the loaded section.
- Bending Moment Diagram:
- The bending moment increases linearly over the length of the applied uniform load and reaches its maximum value at the fixed end.
- After the distributed load section ends, the bending moment remains constant until the free end of the beam.
- The maximum bending moment at the fixed end is given by \( M_A = \frac{w \cdot b^2}{2} \).
- Deflection: The maximum deflection at the free end of the beam is influenced by the load intensity and length of the applied load. The deflection can be calculated using the formula for deflection due to a uniform load: \[ \delta_{\text{max}} = \frac{w \cdot b^4}{8EI} \] where \( E \) is the modulus of elasticity and \( I \) is the moment of inertia of the beam's cross-section.
Applications
- Structural Engineering: Common in beams where the load is localized at the free end, such as cantilevered beams supporting equipment or other components near the end of the beam.
- Mechanical Systems: Found in situations where the load is concentrated at or near the free end of components like cantilever arms or mechanical supports.
- Construction: Used in the analysis of cantilever beams where loads such as partition walls or storage are placed near the free end of the beam.
Formula
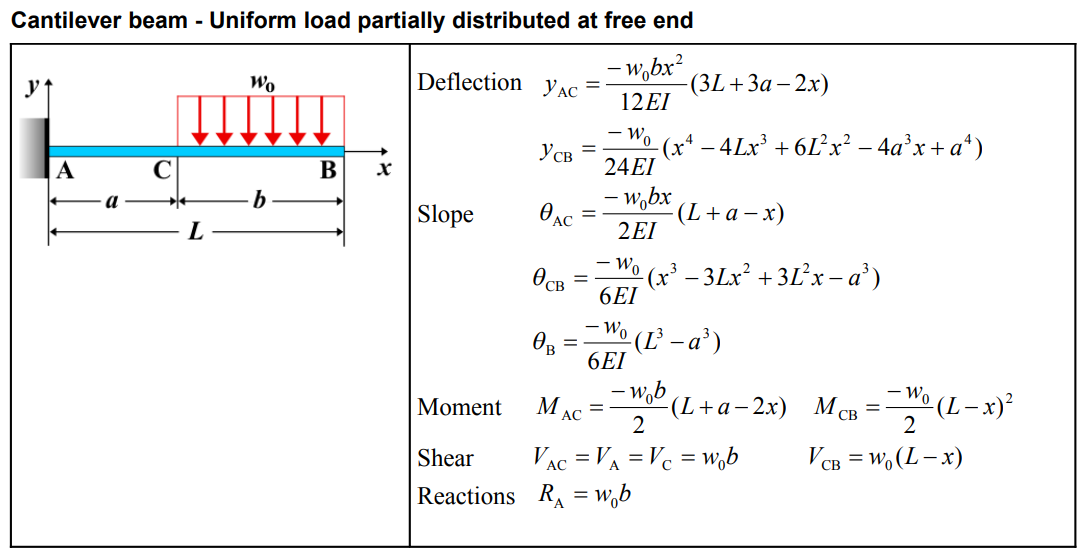
| Category | Formula |
|---|---|
| Deflection (\( y_{AC} \)) | \[ y_{AC} = \frac{-w_0 b x^2}{12EI}(3L + 3a - 2x) \] |
| Deflection (\( y_{CB} \)) | \[ y_{CB} = \frac{-w_0}{24EI}(x^4 - 4Lx^3 + 6L^2x^2 - 4a^3x + a^4) \] |
| Slope (\( \theta_{AC} \)) | \[ \theta_{AC} = \frac{-w_0 b x}{2EI}(L + a - x) \] |
| Slope (\( \theta_{CB} \)) | \[ \theta_{CB} = \frac{-w_0}{6EI}(x^3 - 3Lx^2 + 3L^2x - a^3) \] |
| Slope at B (\( \theta_B \)) | \[ \theta_B = \frac{-w_0}{6EI}(L^3 - a^3) \] |
| Moment (\( M_{AC} \)) | \[ M_{AC} = \frac{-w_0 b}{2}(L + a - 2x) \] |
| Moment (\( M_{CB} \)) | \[ M_{CB} = \frac{-w_0}{2}(L - x)^2 \] |
| Shear (\( V_{AC} \), \( V_A \), \( V_C \)) | \[ V_{AC} = V_A = V_C = w_0 b \] |
| Shear (\( V_{CB} \)) | \[ V_{CB} = w_0(L - x) \] |
| Reactions (\( R_A \)) | \[ R_A = w_0 b \] |
Definitions
| Symbol | Physical quantity | Units |
|---|---|---|
| E·I | Flexural rigidity | N·m², Pa·m⁴ |
| y | Deflection or deformation | m |
| θ | Slope, Angle of rotation | - |
| x | Distance from support (origin) | m |
| L | Length of beam (without overhang) | m |
| M | Moment, Bending moment, Couple moment applied | N·m |
| P | Concentrated load, Point load, Concentrated force | N |
| w | Distributed load, Load per unit length | N/m |
| R | Reaction load, reaction force | N |
| V | Shear force, shear | N |
 Home
Home Back
Back