Cantilever beam - Concentrated load P at any point Calculator

Deflection Yac:

Deflection Ycb:

Deflection Ymax:

Slope θac:

Slope θcb:

Slope θc:

Slope θb:

Moment Mac:

Moment Mcb:

Moment Mc:

Moment Mb:

Moment Ma:

Moment Mmax:

Shear Vac:

Shear Va:

Shear Vc:

Shear Vcb:

Shear Vb:

Reactions Ra:

Cantilever Beam - Concentrated Load \( P \) at Any Point

A cantilever beam is a structural element fixed at one end and free at the other. When a concentrated load \( P \) is applied at any point along the beam, it induces specific effects such as shear force, bending moment, and deflection. Unlike a couple moment, a concentrated load generates both a reaction force and a bending moment at the fixed support.

Key Concepts

Concentrated Load \( P \): A single force applied at a specific point along the beam, measured in units of force (e.g., N or lb).
Fixed End: The end rigidly attached to a support, resisting both rotation and translation.
Free End: The unsupported end that experiences maximum deflection due to the applied force.
Shear Force: Abruptly changes at the point of load application, influencing the shear force diagram.
Bending Moment: Varies along the beam, with the maximum moment occurring at the fixed end.
Deflection: The displacement of the beam, dependent on the load position and magnitude.

Behavior of the Cantilever Beam

Reaction Forces:
- At the fixed end, the beam generates a reaction force \( R_A = P \) to balance the external load.
- A reaction moment \( M_A = P \cdot a \) is developed, where \( a \) is the distance from the fixed end to the applied load.
Shear Force Diagram:
- Shear force remains constant between the fixed end and the point of load application.
- At the point of application, the shear force decreases abruptly by \( P \).
- Beyond the load application point, the shear force remains zero.
Bending Moment Diagram:
- Decreases linearly from the fixed end to the point of load application.
- The maximum bending moment at the fixed end is \( M_A = P \cdot a \).
- Beyond the load application point, the bending moment decreases to zero at the free end.
Deflection: Maximum at the free end, calculated using beam deflection formulas.

Applications

Structural Engineering: Used in bridges, balconies, and overhanging beams in buildings.
Mechanical Systems: Applied in robotic arms, levers, and cantilevered machine components.
Construction: Helps determine the load-bearing capacity and stability of cantilevered structures.

Formula

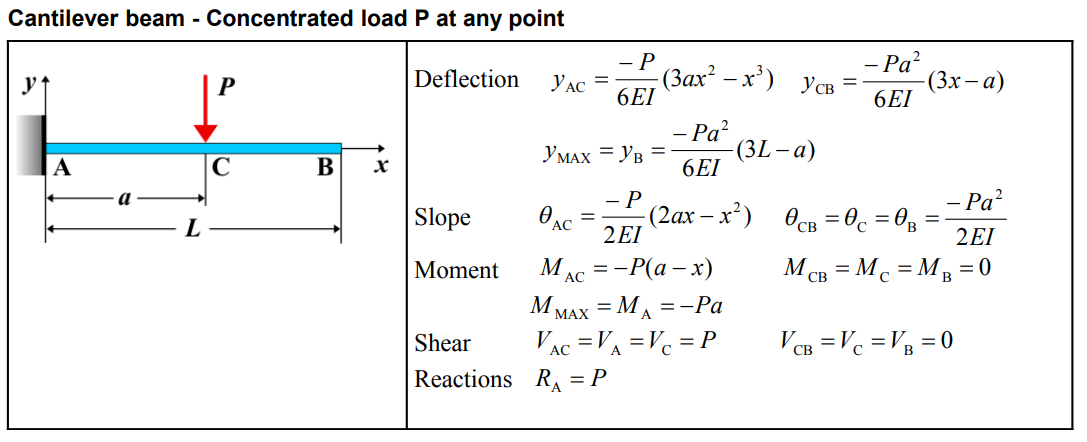
Deflection \(y\)	\(y_{AC} = \frac{6EI}{-P} (3ax^2 - x^3)\)	\(y_{CB} = \frac{6EI}{-Pa^2} (a-x)^2(3x-a)\)
Deflection at \(x = L\) (\(y_{MAx} = y_B\))	\(y_{MAx} = y_B = -\frac{Pa^2}{6EI}(3L-a)\)
Slope \(\theta\)	\(\theta_{AC} = -\frac{P}{2EI}(2ax - x^2)\)	\(\theta_{CB} = \theta_C = \theta_B = -\frac{Pa^2}{2EI}\)
Moment \(M\)	\(M_{AC} = -P(a-x)\)	\(M_{CB} = M_C = M_B = 0\)
Moment at \(x = a\) (\(M_{MAx} = M_A\))	\(M_{MAx} = M_A = -Pa\)
Shear \(V\)	\(V_{AC} = V_A = V_C = P\)	\(V_{CB} = V_C = V_B = 0\)
Reactions \(R\)	\(R_A = P\)

Definitions

Symbol	Physical quantity	Units
E·I	Flexural rigidity	N·m², Pa·m⁴
y	Deflection or deformation	m
θ	Slope, Angle of rotation	-
x	Distance from support (origin)	m
L	Length of beam (without overhang)	m
M	Moment, Bending moment, Couple moment applied	N·m
P	Concentrated load, Point load, Concentrated force	N
w	Distributed load, Load per unit length	N/m
R	Reaction load, reaction force	N
V	Shear force, shear	N